اصل موضوع گسترش - نسخه‌ی قابل چاپ +- انجمن های تخصصی فلش خور (http://www.flashkhor.com/forum) +-- انجمن: علم، فرهنگ، هنر (http://www.flashkhor.com/forum/forumdisplay.php?fid=40) +--- انجمن: تحصیلات دانش آموزی و دانشجویی (http://www.flashkhor.com/forum/forumdisplay.php?fid=64) +--- موضوع: اصل موضوع گسترش (/showthread.php?tid=282251)

اصل موضوع گسترش - The moon - 22-04-2020 یکی از مفاهیم اصلی در نظریه مجموعه‌ها که در بررسی‌های کاملا اصل موضوعی از جمله عمده‌ترین مفایم اولیه و تعریف نشده محسوب می‌شود مفهوم تعلق یا عضویت است. اگر A یک مجموعه باشد و x متعلق A باشد (x عنصر A است یا A شامل x است) می‌نویسیم 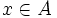. نماد 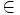 عضویت است و برگرفته از حرف یونانی ε (اپسیلون) است و توسط پئانو مورد استفاده قرار گرفته شده است. کی از روابط مهم میان مجموعه‌ها که تا حدی مقدماتی تر از تعلق است، تساوی دو مجموعه است. اگر دو مجموعه A و B برابر باشند می‌نویسیم A=B و در غیر این صورت می‌نویسیم A≠B. - حال این سوال پیش می‌آید که چه هنگام دو مجموعه را مساوی می‌گوییم؟ برای پاسخ به این سوال اصل موضوعی بنا می‌کنیم که به درستی رابطه بین تساوی و تعلق را در مجموعه‌ها نشان می دهد. دو مجموعه با هم مساوی‌اند اگر و فقط اگر دارای عناصر یکسان باشند. بیان دیگری از اصل موضوع فوق این است که هر مجموعه با گسترش خود (اعضای خود) دقیقا مشخص می‌شود. همچنین با توجه به مفهوم زیرمجموعه می‌توان اصل موضوع گسترش را به گونه‌ای دیگر فرمول بندی نمود. می‌دانیم که اگر مجموعه A زیرمجموعه، مجموعه B باشد می‌نویسیم 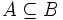 این بدان معنی است که هر عضو A، متعلق به B نیز می‌باشد. حال اگر برای هر دو مجموعه دلخواه A و B داشته باشیم  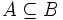و 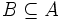 آنگاه بدیهی است که طبق تعریف هر عضو A در B و هر عضو B در A موجود است و لذا اعضای A و B یکسان هستند. پس: دو مجموعه باهم مساویند اگر و فقط اگر هر یک زیر مجموعه دیگری باشد. به عبارت دیگر اگر A و B دو مجموعه باشند A=B اگر و فقط اگر 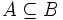  و 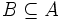. پس اصل موضوع گسترش به ما کمک می‌کند که بدانیم چه موقع دو مجموعه‌ با هم برابرند. با توجه به این اصل همواره اثبات تساوی دو مجموعه به دو بخش تقسیم می‌شود که باید در هر قسمت نشان دهیم هر یک از مجموعه‌ها زیرمجموعه دیگری است. /رشد